寻找最值
高中求最值:
- 求导,寻找导数为0的点
- 求端点的函数值,把这些点放一块比较找出最值
为什么这样做可以找到最值?他的依据是什么?
先说说连续和可导的关系
大家应该都背过自行车那个顺口溜:
连续不一定可导,可导必连续
但其实,我只需要帮你理清连续可导究竟是怎么回事,你就不需要这个拐杖了
连续
就是不中断,函数连续就是一条没有中断的曲线
$y=sin(x)$连续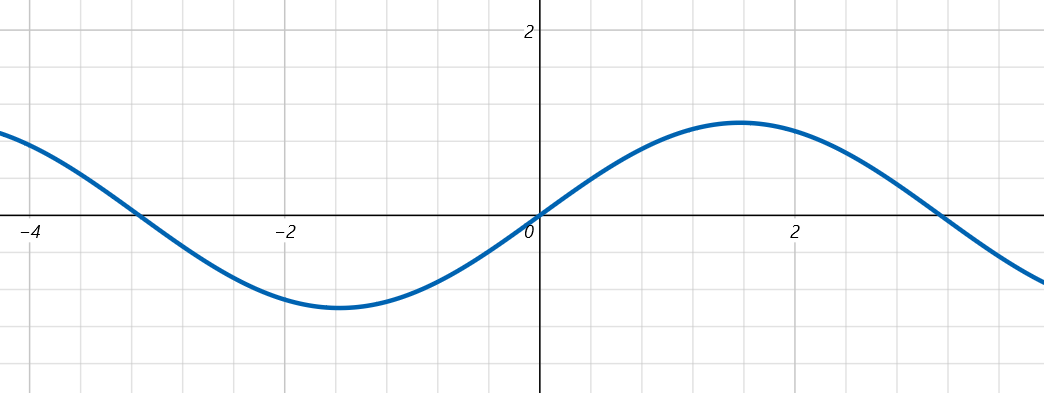
$y=|x|$也连续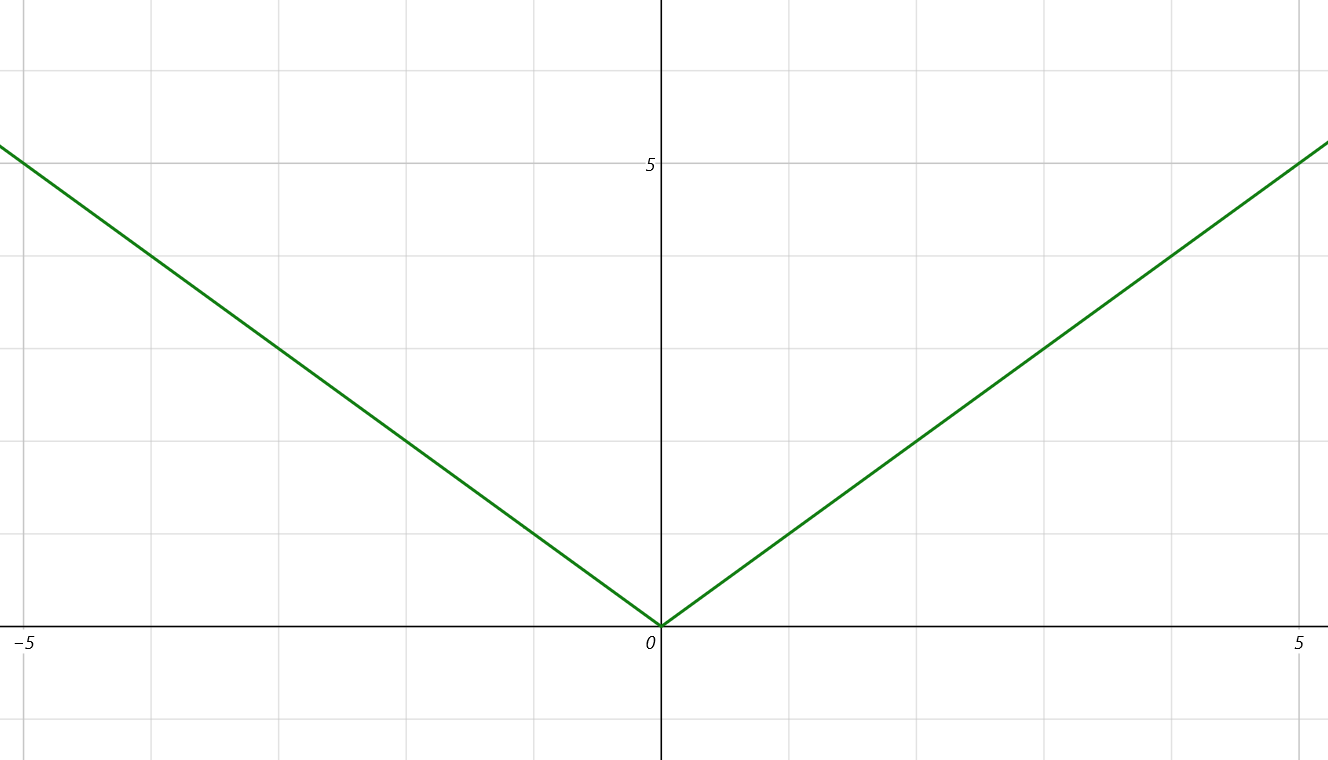
可导
一段连续且平滑的曲线
$y=sin(x)$可导
$y=|x|$就不再可导,因为他有尖锐的地方(画不出来切线)
初中可没学导数,那时候接触的都是可导的函数,所以你还记得当时画图时有这样一句话
在平面直角坐标系内,将点依次描出来。
用光滑的曲线将这些点连接起来,得到函数的图像。
总结一下,连续>可导
现在我们来探讨:
连续的函数具有什么性质?在连续的基础上可导,又能得出什么样的结论?
这部分在教材中对应第三章‘微分中值定理和导数的应用’
让我以求最值为引,帮你弄清:那堆中值定理们究竟在讲什么
连续的结论
最值存在性定理
在闭区间上连续的函数在该区间上有界且一定能取得它的最大值和最小值
本文重点在求最值,所以介值定理(零点定理)先不说
最值存在性定理就俩关键词:闭区间,连续。也就是闭连
现在我们知道了闭连有最值,那么最值在哪里呢?
把最值可能出现的整个范围分成三段
两个端点
可导点
不可导点
何谓极值?极值和最值有何区别?
极值为局部,最值为全局,区别在于存在的范围
如果我们以时间为轴,把我们的人生看作波荡起伏的函数
把函数中最大的那个值当作人生高光,那我们一生中做的众多选择都是在追求这个点能够更高,也就是寻找我们人生的最优解。
比如我的两个选择形成了两个函数A和B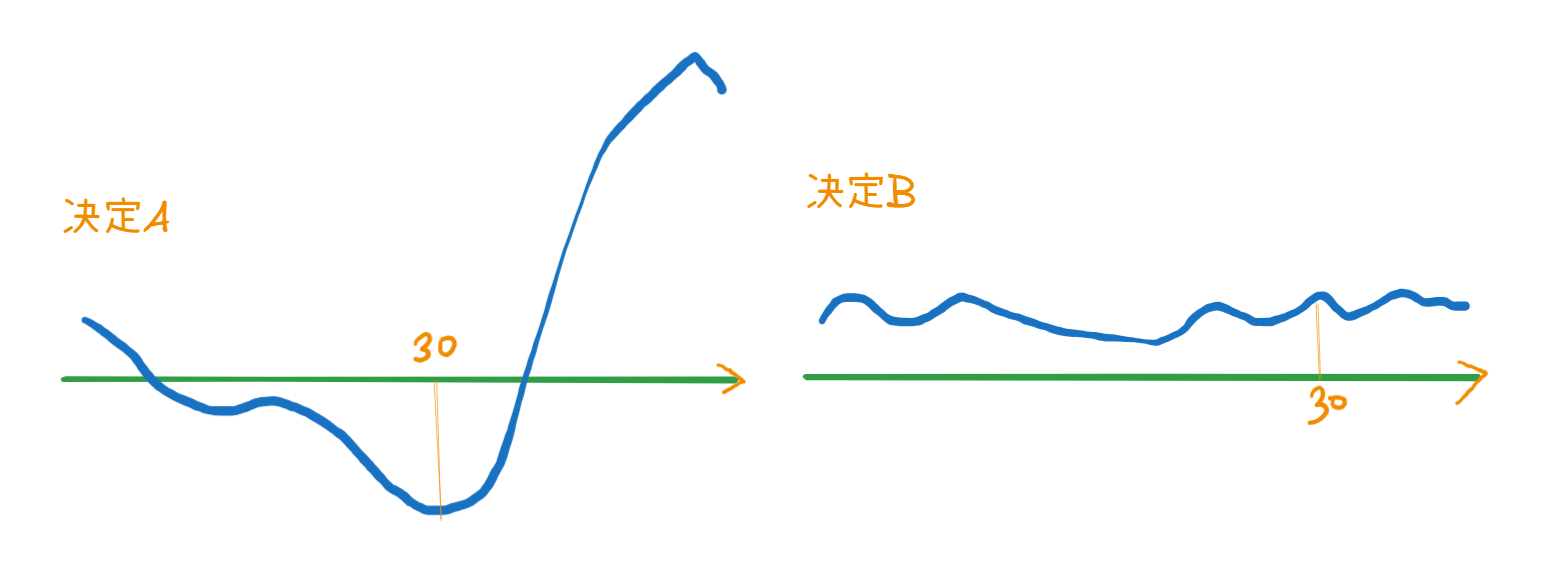
函数A是标准的‘天将降大任于斯人也,必先苦其心志’
如果只将人生高度作为衡量标准,我们会选择决定A
可是作为茫茫众生,我们无法找到这个最值,因为从上文所列的,最值的范围来看
我们无法一眼看到生命的尽头,无法看到那个多年后的高峰
我们眼中看到的图像是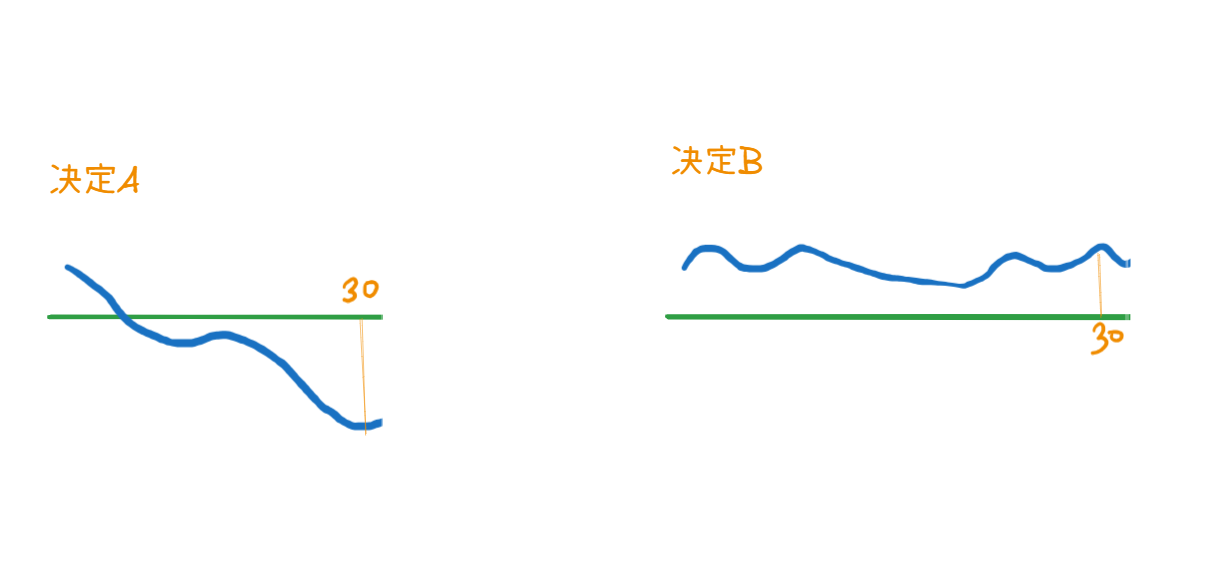
我们看到的这个$A(30)$函数值,叫极值,也就是说,极值的存在范围不包含两个端点
让我们看看数学家是怎样刻画极值不同于最值的局部性的?
极值
极值是一个函数的极大值或极小值。如果一个函数在一点的一个邻域内处处都有确定的值,而以该点处的值为最大(小),这函数在该点处的值就是一个极大(小)值。
邻域:以某个点为中心的开区间
这个定义要求范围是对称的,左右两边都有的,所以注定了极值无法取端点,因为在端点处的范围是单侧(在人死了那一点,人生就结束了,没有下文了)
总结一下: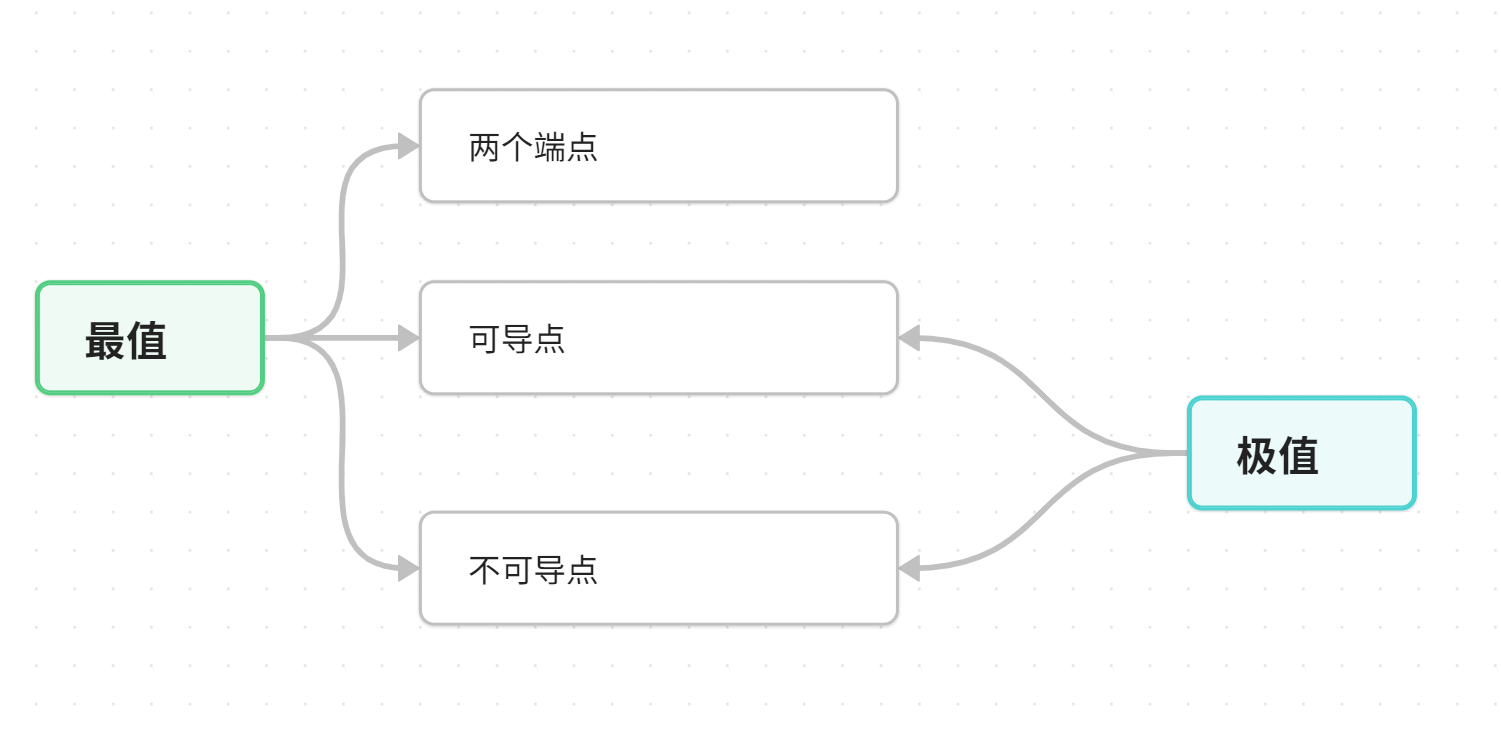
即:最值出现在端点和极值点上
可导的结论
连续>可导。连续的结论,可导都包含。比如:最值存在性定理,介值定理
费马引理
条件:1️⃣函数$f(x)$在某点x0处是极值2️⃣函数在此点可导
结论:此点导数为0
费马引理表明了极值在可导点具有的性质:导数为0
证明思路:
最值有三个可能出现的地方,太多,我只研究一个,即可导的那个
1️⃣极值点这个条件就去掉了两个端点,2️⃣把不可导点去掉
当这个可导点是极值时,他就是最大的那个,左右两边的函数值都比他小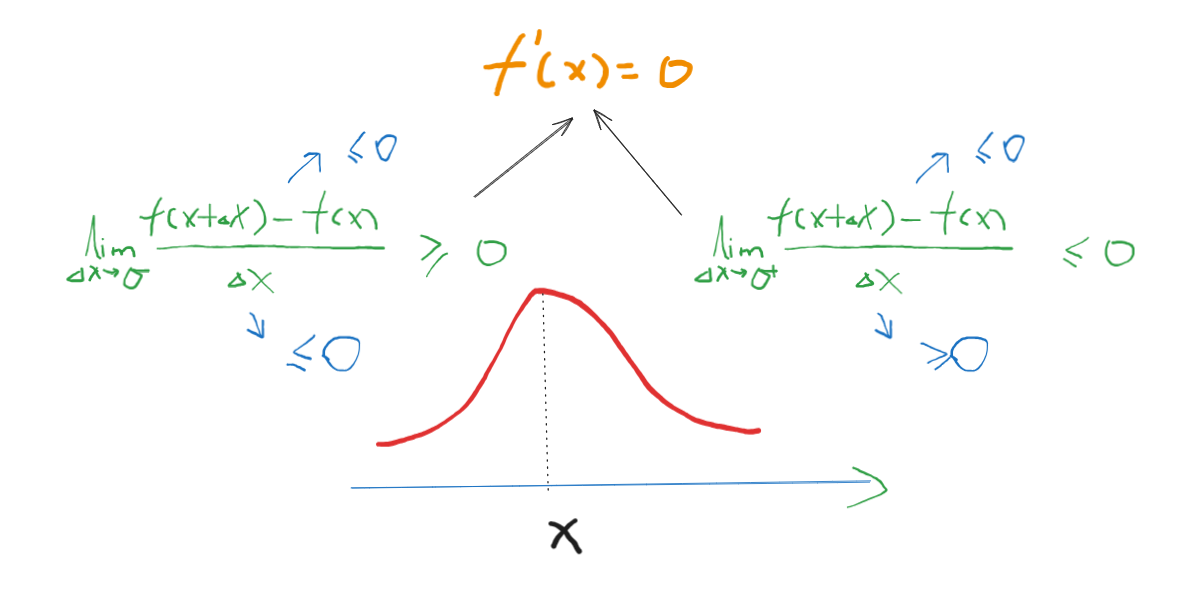
注意
极值点导数为零也就是驻点,但反过来逆命题,导数为零(驻点)可不一定是极值点
例如: $y=x^{3}$
高中时求最值是反着用的费马引理
先求导数为0的点缩小极值点的候选范围(即先找驻点,再验证)——可导点
计算端点函数值——两个端点
发没发现我们并没有计算——不可导点
应该是因为高中接触的函数都可导
插:何谓不可导
在连续的情况下(要是都不连续,还谈什么可导)
极限是工具,导数用极限定义,极限不存在,导数就不存在喽
极限存在要满足的两个条件:
1.左右极限存在
2.左右极限相等
极限(导数)不存在:
1.左右极限(导数)不相等
$y=|x|$
2.无限震荡
$\lim_{x \to 0} sin\frac{1}{x}$
3.趋向无穷
说了半天:连续函数闭区间存在最值,怎么找最值
可是哪些函数是连续的呢???
好消息,咱们学的五大基本初等函数在它们的定义域内都是连续的
幂,指,对,三角,反三角
根据教材的定理1和定理4,一切初等函数在其定义域内自动连续
初等函数
由基本初等函数经过有限次四则运算(加、减、乘、除)和有限次函数复合得到的函数。


费马引理求最值告一段落,真正的中值定理还未开始
未完待续,且看下篇


